

Article of the Month - November 2019 |
Pasi Häkli, Finland, Martin Lidberg, Sweden, Lotti Jivall, Sweden, Holger Steffen, Sweden, Halfdan P. Kierulf, Norway, Jonas Ågren, Sweden, Olav Vestøl, Norway, Sonja Lahtinen, Finland, Rebekka Steffen, Sweden and Lev Tarasov, Canada
 |
 |
 |
 |
 |
| Pasi Häkli | Martin Lidberg | Lotti Jivall | Holger Steffen | Halfdan P. Kierulf |
 |
 |
 |
 |
 |
| Jonas Ågren | Olav Vestøl | Sonja Lahtinen | Rebekka Steffen | Lev Tarasov |
This article in .pdf-format (15 pages)
This article was presented at the FIG Working Week 2019 in Vietnam. The paper describes the latest development of horizontal intraplate velocity model. The horizontal velocities of the model are comprised of the BIFROST GNSS velocity solution and a new GIA model.
In the northern Europe, Fennoscandian region with its surroundings is affected by the Glacial Isostatic Adjustment (GIA) resulting in intraplate crustal motions up to a few millimeters per year in horizontal coordinates and up to a centimeter per year in heights. The national reference frames in Nordic and Baltic countries are plate-fixed and based on European Terrestrial Reference System 1989 (ETRS89) and European Vertical Reference System (EVRS), as regulated by the European Union’s Inspire directive. In maintenance of the national reference frames and in the most accurate georeferencing applications the GIA effect must be accounted for. The Nordic countries have a long tradition on studying the GIA (or land uplift) phenomenon. Latest efforts have been conducted in collaboration under the Nordic Geodetic Commission (NKG) and have resulted in some common Nordic-Baltic land uplift and deformation models. For example, the NKG2005LU model has been used e.g. in levelling adjustments as the basis for Nordic European Vertical Reference Frame (EVRF) realizations and the NKG_RF03vel model e.g. for transforming International Terrestrial Reference Frame (ITRF) coordinates accurately to national ETRS89 realizations.
In this paper we describe the latest development of horizontal intraplate velocity model. The horizontal velocities of the model are comprised of the BIFROST GNSS velocity solution and a new GIA model NKG2016GIA_prel0907. The GIA velocities were first aligned from a GIA frame to a geodetic reference frame by a Helmert fit using GNSS velocities. Then the final adjustment was done with least-squares collocation also accounting for the GNSS velocity uncertainties. We describe the methodology and show results of the derived model. Through the results we affirm that the methodology is adequate. The derived model velocities agree at an approx. 0.15 mm/a level with the GNSS velocities based on long time series. However, based on other findings in this paper, we have selected to continue the work and consider the model presented herein as a preliminary model.
In northern Europe, i.e. the Fennoscandian area, the glacial isostatic adjustment, GIA (or postglacial rebound, PGR), process, which is the Earth's response to the waxing and waning of ice sheets, causes internal deformations to the Eurasian plate. The magnitude of GIA reaches up to about 1 cm/a in the vertical, and a few millimetres per year in the horizontal direction, see e.g. Lidberg et al. 2010.
As a common challenge, GIA has been studied in the last decades within a strong Nordic-Baltic co-operation under the umbrella of the Nordic Geodetic Commission, NKG. The NKG released the vertical land uplift model NKG2005LU in 2005 (Vestøl 2006, Ågren and Svensson 2008). The NKG2005LU model has been used, for instance, for data reductions in computations of the Nordic EVRS (European Vertical Reference System) realizations that are used as official height systems in the Nordic countries. In 2006, the NKG released an NKG_RF03vel model that includes horizontal velocities as well (Nørbech et al. 2008). The vertical velocities of the NKG_RF03vel are those of NKG2005LU_abs (relative to the ellipsoid) and horizontal velocities are based on GNSS station velocities as well as a geophysical GIA model. The 2D+1D NKG_RF03vel model has been used to reduce 3D intraplate deformations e.g. in transformations from global reference frames, like ITRF (International Terrestrial Reference Frame), to national ETRS89 (European Terrestrial Reference System 1989) realizations when best possible accuracy is required (Nørbech et al. 2008, Häkli et al. 2016).
During the years new geodetic data and geophysical models have been released that are filling some gaps in these NKG models. Mostly the NKG models still perform well (see e.g. Häkli et al. 2016) but it became obvious that they can be improved.
In 2016, in the 3rd NKG Joint Working Group Workshop on Land Uplift Modelling it was decided to release a new land uplift model package: NKG2016LU_abs/lev, NKG_RF17vel and NKG2016LU_gdot. NKG2016LU_abs/lev describes vertical land uplift velocities, NKG_RF17vel includes additionally horizontal velocities and NKG2016LU_gdot is a gravity change model. The NKG2016LU model is an update of the NKG2005LU model and it was released in June 2016 (Vestøl et al., submitted). The NKG2016LU model is based on levelling and GNSS data as well as a GIA model. Two separate models for absolute (relative to ellipsoid) and levelled (relative to geoid) uplift were released. Similarly to the NKG_RF03vel model, the NKG2016LU_abs model will be the basis for the vertical velocities of the NKG_RF17vel model. In this paper we present the methodology and first results to derive the horizontal velocities of the NKG_RF17vel model.
Nordic land uplift models use observations from several geodetic measurement techniques and predictions from GIA models. Horizontal velocities of the NKG_RF17vel model are a combination of GNSS (Global Navigation Satellite System) and GIA velocities. The advantage of GNSS data is that it results in absolute velocities in a global terrestrial reference frame (TRF) which can be used for reference frame alignment. GNSS velocities are based on Continuously Operating Reference Stations (CORS) and their sufficiently long observation time series. CORS networks, however, are typically pretty sparse for describing local motions and therefore need to be amended with other data to densify the velocity field. GIA models (along with the chosen combination procedure) provide details for the GNSS velocity field (”thus fill the gaps”).
The computation and analysis of the CORS data is performed with the software «GPS Analysis software of MIT» (GAMIT) (Herring et al. 2015). In the analysis, we use 10-degree cut-off elevation angle, elevation dependent weighting, the igs08.atx antenna phase center model, the Vienna Mapping Function (VMF1) (Boehm et al. 2006) tropospheric mapping function and the FES2004 ocean loading model (Scherneck 1991). Atmospheric tidal loading is included, but no model for the non-tidal atmospheric loading nor a model for higher order ionospheric disturbances is used. To optimize the data processing, we divide the network in several sub-networks and analyze them on a daily basis. We combine the daily sub-networks to one daily solution. To ensure a good connection to the global reference frame, we also analyze global sub-networks and combine them with the regional networks of CORS.
We provide the GNSS results in IGb08, a GNSS-based realization of ITRF2008 (Altamimi et al. 2011) from IGS and updated to include changes in phase center model used for analysis, as well as changes in the network after the realization of ITRF2008 but without changing the datum definition (scale, origin and orientation). The afterwards published velocities of ITRF2014 (Altamimi et al. 2016) solution agree at a level of 0.3 mm/a with velocities in ITRF2008. Therefore, giving this quite low discrepancy, the velocities are kept in ITRF2008.
We transform the daily GAMIT network solution to the IGb08 reference frame in a two-step procedure. First, we make a global realization where the daily minimal constrained network is transformed to IGb08 using 64 globally distributed GNSS stations as reference. For the regional solution, we repeat the procedure using all the Nordic and Baltic stations, except a few stations with outlier behavior, as reference stations with coordinates obtained from the global solution (see Kierulf 2017 for more details). This two-step procedure using this dense-network stabilization is more robust since we have a stronger realization of the frame on each day. This approach also removes most of the spatially correlated noise on the regional level (so-called common mode error).
We then use the software Cheetah to estimate velocities, annual and semi-annual signals as well as their corresponding uncertainties from the time series of the CORS. Cheetah is a successor of the time series analysis software CATS (Williams 2008) and uses the differencing method described in Bos et al. (2008). To compensate for coordinate changes for all known antenna and radome changes, we include Heaviside step functions. We also include such functions when jumps in the time series are obvious after visual inspection. In the time series analysis, we assume the presence of power-law noise and estimate the spectral index. This ensures more realistic velocity uncertainties (see e.g. Williams et al. 2004). Based on a 3-sigma criterion, we remove outliers (where snow accumulation on antenna installations are the dominant cause for outliers at high northern latitudes) in a preliminary analysis using an in-house least squares program.
As a result we have GNSS station velocities and uncertainties in
IGb08 for 179 stations that are based on a minimum of three years of
data, in most cases much more; the average time span is 11.4 years (Fig.
1). To obtain intraplate GNSS velocities, the rigid Eurasian plate
motion was removed from the IGb08 velocities with the Euler pole defined
by the ITRF2008 plate motion model, ITRF2008-PMM (Altamimi et al. 2012).
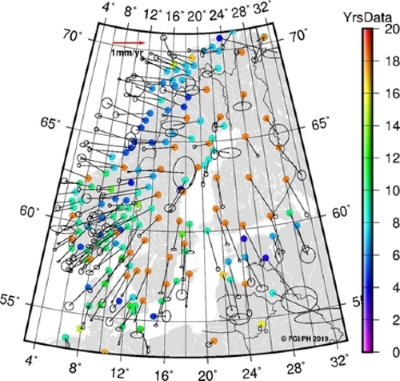
Figure 1. BIFROST GNSS velocities (vectors), their standard uncertainties (ellipses) and length of time series (colored circles).
The GIA model was computed using the software ICEAGE (Kaufmann, 2004) which applies the viscoelastic normal-mode method (Peltier, 1974) and where the sea-level equation is solved iteratively. A set of spherically symmetric (1D), compressible, Maxwell-viscoelastic earth models with four layers is generated. They differ in five parameters: lithospheric and asthenospheric thickness, asthenospheric, upper and lower mantle viscosity. Rheological parameters for the elastic structure are based on PREM (Dziewonski & Anderson, 1981). Table 1 summarizes the tested values for the five parameters. Their range covers former results from the computation of the land uplift model NKG2016LU (Vestøl et al., submitted).
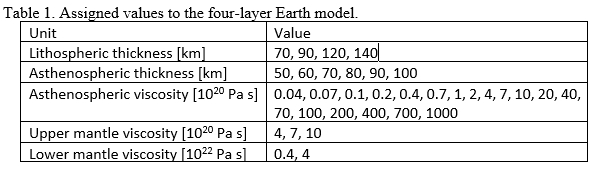
Table 1. Assigned values to the four-layer Earth model.
We use a set of 25 different ice-sheet history model as surface loads. These ice sheet chronologies for Fennoscandia, the Barents/Kara seas and the British Isles are versions of GLAC (Tarasov et al. 2012, Root et al. 2015, Nordman et al. 2015). Combination of these 25 ice models with 2736 Earth models results in 68,400 unique GIA models to test. For each GIA model, we calculate vertical elevation change (i.e. the absolute land uplift), horizontal motion and sea-level change at selected times during and after the last glaciation. This allows comparison of our predictions with the BIFROST-derived GNSS result and a large dataset of geological and paleontological relative sea-level (RSL) observations for northern Europe (see Vestøl et al., submitted). The observed velocity field is transformed into the GIA (model) frame (Kierulf et al. 2014). We then compare and calculate the misfit of the models to the observations with root-mean-square fitting:
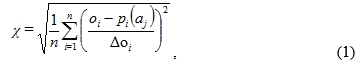
where, n is the number of observations considered, oi is the observed RSL or BIFROST-derived velocity value, pi(aj) is the predicted RSL or velocity for a specific GIA model aj, and Δoi is the data uncertainty. The minimum value of χ within the parameter range eventually results in the best-fitting Earth model ab. As we are interested in a model that fits both the GNSS and RSL data simultaneously, we calculate a linear weighted combination of the misfit for GNSS data χGNSS and the misfit for RSL data χRSL to achieve a total misfit χtotal. It is generally recommended to put more weight on the RSL data to promote a unique solution (Vestøl et al., submitted). After some tests, we give four times higher weight to RSL data than to the GNSS data.
The best-fitting GIA model is called NKG2016GIA_prel0907. It consists of a 120 km lithospheric thickness, a 90 km thick asthenosphere with a viscosity of 1022 Pa s, an upper-mantle viscosity of 7 x 1020 Pa s, a lower mantle viscosity of 4 x 1022 Pa s and uses the GLAC ice history model #71340. The horizontal velocity field of NKG2016GIA_prel0907 is shown in Fig. 2.
As the GIA velocities of the NKG2016GIA_prel0907 model are expressed in a ”GIA frame” (Kierulf et al. 2014), they need to be re-aligned to a geodetic reference frame. As mentioned in the previous section, GNSS velocities can be used for reference frame alignment. As we want to preserve the internal geometry of the GIA velocity model, we use a Helmert fit with three rotations only to re-align the GIA velocities to the GNSS velocities. This corresponds to an Euler pole approach and affects only the horizontal velocities that we are interested in.
For alignment we select a subset of ”best” BIFROST stations considering e.g. homogeneous distribution and length and discontinuities of the GNSS time series. As a result 66 stations were used for alignment of the GIA velocities (orange circles in Fig. 3). After the reference frame alignment the GIA velocities agree with the GNSS velocities at approx. 0.2-0.3 mm/a level (1σ), see Fig. 3. The uncertainty level of the BIFROST velocities is, however, smaller and therefore we aim at further improving the alignment. This is done with a least-squares collocation.
After the Helmert fit, we use GNSS and aligned GIA velocities together with GNSS velocity uncertainties as input to a least-squares collocation, LSC. The LSC was performed with the GRAVSOFT software’s routine GEOGRID component-wise, i.e. for North and East velocities separately.
It is important to have as realistic standard uncertainties as possible for the GNSS velocities in order to align the model well to the GNSS velocities. By using power-law noise and estimating spectral index for the uncertainty estimation, we consider the BIFROST velocity uncertainties to be as realistic as possible. However, we still set the minimum velocity uncertainty to 0.1mm/a in the LSC to avoid unncessary instabilities in the collocation procedure.
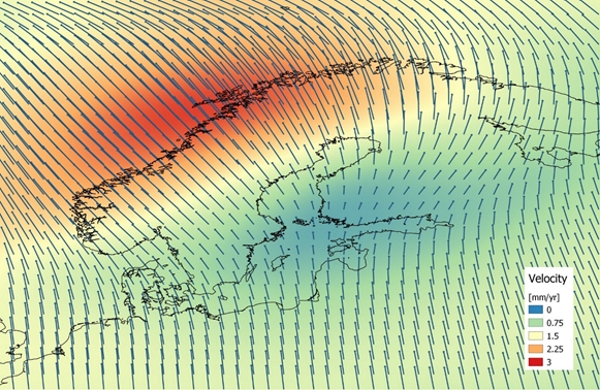
Figure 2. NKG2016GIA_prel0907 velocities.
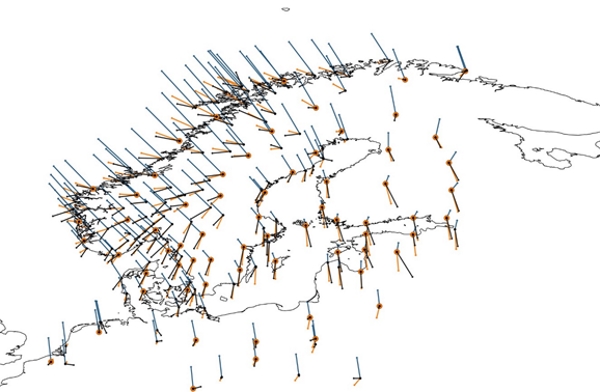
Figure 3. BIFROST (black vectors), NKG2016GIA_prel0907 (blue vectors), re-aligned GIA (orange vectors) velocities and stations used for alignment (orange circles).
GRAVSOFT models the covariance function with a second order Gauss-Markov model where the user has to specify the correlation length. Considering the density of CORS stations, expectation of a smooth surface and the correlation length used in the NKG2016LU model, we select the same 150 km correlation length for the horizontal velocities. Farther away from CORS stations (basically outside the Nordic-Baltic region) the model velocities converge to the aligned GIA velocities.
We use the ”remove-interpolate-restore” method meaning that we first compute the velocity difference of the Helmert-fitted GIA velocities and the GNSS velocities (remove GIA from the GNSS velocities), then apply LSC to the velocity differences (collocation signal) and finally restore the Helmert-fitted GIA velocities to the collocation signal to get the intraplate model. The LSC also provides uncertainties for the obtained signal. The collocation uncertainties are guided by the GNSS station velocity uncertainties as well as the chosen correlation length. The estimated signal, collocation uncertainty and the resulting intraplate model are shown in Figs. 4, 5 and 6, respectively.
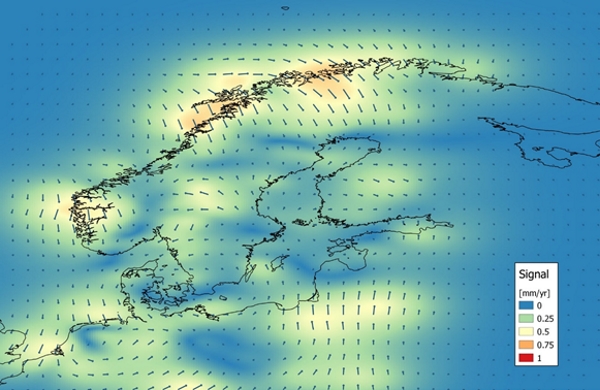
Figure 4. Least-squares collocation signal, i.e. correction on top of the aligned GIA velocities.
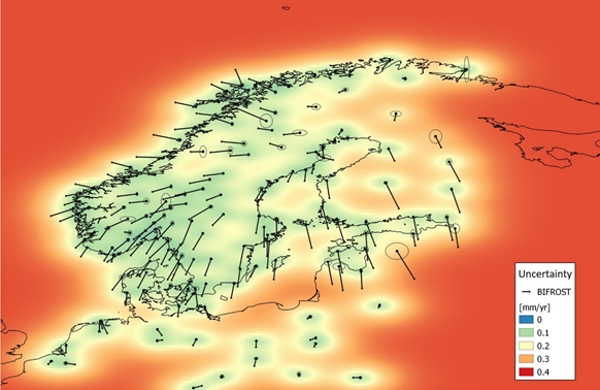
Figure 5. Least-squares collocation standard uncertainty.
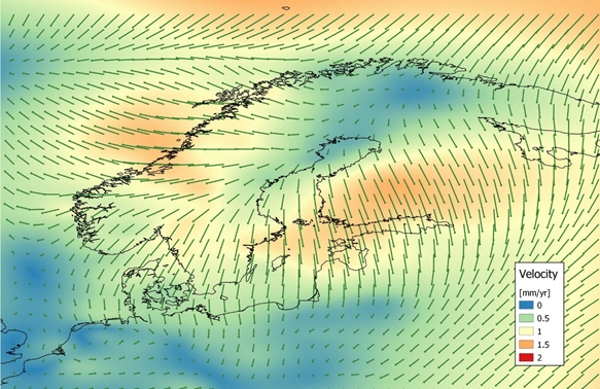
Figure 6. Velocities of the horizontal intraplate model.
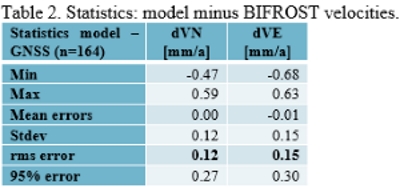
We compare the derived model and the BIFROST velocities in order to verify the solution. Fig. 7 shows both velocities and BIFROST velocity uncertainties. The model velocities converge to the BIFROST velocities when the BIFROST velocity uncertainties are low and less with higher uncertainties. The agreement, by means of root-mean-square (RMS) of differences, has improved after the LSC from a 0.2-0.3 mm/a level to 0.12 mm/a and 0.15 mm/a for North and East velocities, respectively (see Table 2). Consequently, the model agrees with the GNSS velocities at the uncertainty level meaning optimum alignment with the available data.

Figure 7. BIFROST (black vectors), model (green vectors) velocities and BIFROST velocity uncer tainties (black ellipses).
Table 2. Statistics: model minus BIFROST velocities.
Comparison in the previous section verifies the success of the alignment of the model with respect to the used data. However, this represents ”internal” accuracy of the model and it is therefore useful to compare the model to some external data, too. We use a velocity solution of the EPN (EUREF Permanent Network) densification project that was released in 2018 (EPN 2019) for comparison. It covers whole Europe with more than 3000 GNSS stations.
The EPN densification velocities are expressed in ETRF2000. Therefore, we transformed our model to ETRF2000 before comparison. Then, we interpolated the model velocities for the EPN densification stations. There are almost 600 stations within the coverage of the model, however, it must be noted that most of these are outside the Nordic-Baltic region where the NKG model is guided rather by the GIA model than by GNSS observations.
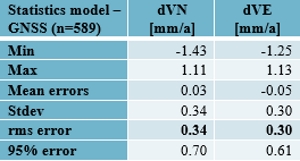
The agreement, by means of RMS of the differences, is at the level of 0.3 mm/a for the whole area of the model (Table 3). The agreement is, however, better in the Nordic-Baltic area, see Fig. 8. This shows that the model is working very well where the model is based on sufficiently dense GNSS velocities. However, some less accurate regions can immediately be seen from Fig. 8. It is obvious that the model suffers from sparse GNSS data in the Baltic area as well as south to the Baltic Sea e.g. in northern Germany and Poland. However, in this direct comparison we did not consider any uncertainties which may explain part of the differences. This is due to the fact that only unrealistic white-noise type of uncertainties for the EPN densification velocities are currently available.
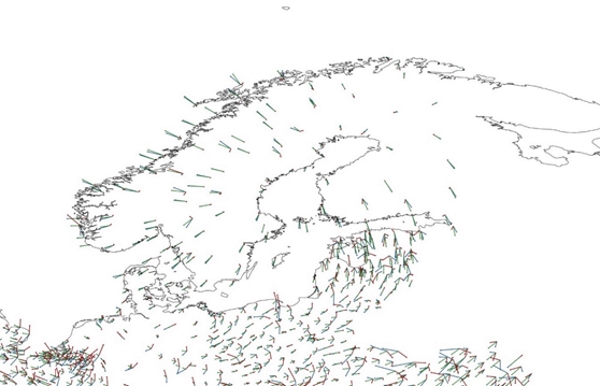
Figure 8. Model (green vectors), EPN densification (blue vectors) velocities and their difference (red vectors).
Table 3. Statistics: model minus EPN densification velocities.
We have presented the methodology for development of a new horizontal land uplift model for northern Europe. The model is based on GNSS and GIA velocities and is a result of two consecutive alignments for the GIA velocities. First, we do the reference frame alignment to get the GIA velocities to a geodetic reference frame and then further align the resulted velocities to agree with the GNSS velocities to a level of GNSS uncertainties. We have shown this method to be successful but also identified some small weaknesses in the current data set. The model is lacking GNSS data in the Baltic region and south of the Baltic Sea and in these areas the underlying GIA model is pronounced showing slightly less accurate velocities. The model would benefit from extra data in these areas. NKG is therefore preparing an updated GNSS velocity and uncertainty solution for the Nordic-Baltic area that will include more stations in the Baltic area as well as longer time series. This solution will be released in the near future. Based on this and findings in this paper, we will improve the model and therefore we consider this model presented herein only as a preliminary model, NKG_RF17vel_prel. We continue the work based on the findings in this paper.
A major finding is that the deformation pattern of the horizontal velocities exhibits a source region, that is the area where velocities are zero, further North than the location of the land uplift maximum visible in NKG2016LU. Both locations are actually expected to overlap. However, for NKG_RF17vel_prel intraplate velocities are reduced with the ITRF2008-PMM from the IGb08 velocities. This model gives horizontal velocities of a few tenths of mm/a to the area of vertical land uplift maximum. The uncertainty of the absolute plate rotation pole of the Eurasian plate from the ITRF2008-PMM is, by means of WRMS, about 0.3 mm/a for the fit stations (Altamimi et al. 2012). Considering this and the fact that Fennoscandian GIA-affected stations were excluded from the estimation of the Euler pole of the Eurasian plate, the agreement is at the level that can be expected. One could improve this with an additional fit by aligning the zero horizontal velocities to the vertical land uplift maximum. On the other hand, considering usage of the model, it is more likely that the model shall be used with the ITRF plate motion model, cf. Häkli et al. 2016, and therefore it is not meaningful to create a tailor-made solution. Besides, the situation may be different when using other plate motion models. The updated NKG GNSS solution will be expressed in ITRF2014, thus the corresponding ITRF2014-PMM should consequently be used for reducing ITRF2014 velocities to intraplate velocities.
For this model we have used a correlation length of 150 km in the LSC mainly based on the choice made for the vertical NKG2016LU model. We did not perform a covariance analysis for the data but a test with a correlation length of 200 km shows only negligible differences compared to what was presented here. Influence on the model velocities was mainly below 0.05 mm/a for the used BIFROST stations. But as we continue the work, also a covariance analysis will be made before releasing the final model.
In addition, we will produce uncertainties for the model velocities and bring the model into a general use by incorporating it to the NKG transformation scheme similarly as in Häkli et al. 2016.
Altamimi, Z., Collilieux, X., Métivier, L. (2011): ITRF2008: an improved solution of the international terrestrial reference frame. J. Geod. 85, 457-473.
Altamimi Z., Métivier L. and Collieux X., 2012, ITRF2008 plate motion model, J. Geophys. Res., 117, B07402. Doi:10.1029/2011JB008930.
Altamimi, Z., Rebischung, P., Métivier, L., Collilieux, X. (2016): ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. 121, 6109–6131.
Boehm, J., Werl, B., Schuh, H. (2006): Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 111, B02406.
Bos, M.S., Fernandes, R.M.S., Williams, S.D.P., Bastos, L. (2008): Fast error analysis of continuous GPS observations. J. Geod. 82, 157–166, doi:10.1007/s00190-007-0165-x.
Dziewonski, A.M., Anderson, D.L. (1981): Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356.
EPN (2019): EPN densification: http://epncb.oma.be/_densification/ Accessed February 1, 2019.
Herring T.A., King R.W., Floyd M.A., McClusky S.C. (2015): Introduction to GAMIT/GLOBK Release 10.6. User Manual.
Häkli, P., Lidberg M., Jivall L., Nørbech T., Tangen O., Weber M., Pihlak P., Aleksejenko I., and Paršeliunas E., 2016, The NKG2008 GPS campaign – final transformation results and a new common Nordic reference frame, Journal of Geodetic Science. Volume 6, Issue 1, ISSN (Online) 2081-9943, DOI: https://doi.org/10.1515/jogs-2016-0001, March 2016.
Kaufmann, G. (2004): Program package ICEAGE, Version 2004. Manuscript, Institut für Geophysik der Universität Göttingen, 40 pp.
Kierulf, H.P. (2017): Analysis strategies for combining continuous and episodic GNSS for studies of neo-tectonics in Northern-Norway. J. Geodyn. 109, 32-40.
Kierulf, H.P., Steffen, H., Simpson, M.J.R., Lidberg, M., Wu, P., Wang, H. (2014): A GPS velocity field for Fennoscandia and a consistent comparison to glacial isostatic adjustment models. J. Geophys. Res. 119(8), 6613-6629.
Lidberg M., Johansson J. M., Scherneck H.-G. and Milne G. A., 2010, Recent results based on continuous GPS observations of the GIA process in Fennoscandia from BIFROST, J. Geodyn, 50:1, 8–18. Doi:10.1016/j.jog.2009.11.010.
Nordman, M., Milne, G., Tarasov, L. (2015): Reappraisal of the Angerman River decay time estimate and its application to determine uncertainty in Earth viscosity structure. Geophys. J. Int. 201, 811–822.
Nørbech T., Engsager K., Jivall L., Knudsen P., Koivula H., Lidberg M., Madsen B., Ollikainen M. and Weber M., 2008, Transformation from a Common Nordic Reference Frame to ETRS89 in Denmark, Finland, Norway, and Sweden – status report, In: Knudsen P. (Ed.), Proceedings of the 15th General Meeting of the Nordic Geodetic Commission (29 May – 2 June 2006), DTU Space, 68–75.
Peltier, W.R. (1974): The impulse response of a Maxwell earth. Rev. Geophys. Space Phys. 12, 649-669.
Root, B.C., Tarasov, L., van der Wal, W. (2015): GRACE gravity observations constrain Weichselian ice thickness in the Barents Sea. Geophys. Res. Lett. 42, 3313–3320.
Scherneck, H.-G. (1991): A parametrized solid earth tide model and ocean tide loading effects for global geodetic base-line measurements. Geophys. J. Int. 106(3), 677-694.
Tarasov, L., Dyke, A.S., Neal, R.M., Peltier, W.R. (2012): A data-calibrated distribution of deglacial chronologies for the North American ice complex from glaciological modeling. Earth Planet. Sci. Lett. 315–316, 30–40.
Vestøl O., 2006, Determination of postglacial land uplift in Fennoscandia from leveling, tide-gauges and continuous GPS stations using least squares collocation, J Geodesy, 80, 248–258. DOI 10.1007/s00190-006-0063-7.
Vestøl, O., Ågren, J., Steffen, H., Kierulf, H., Tarasov, L. (submitted): NKG2016LU - A new land uplift model for Fennoscandia and the Baltic Region. J. Geodesy.
Williams, S.D.P. (2008): CATS: GPS coordinate time series analysis software. GPS Solutions 12, 147–153. doi:10.1007/s10291-007-0086-4. Williams, S.D.P., Bock, Y., Fang, P., Jamason, P., Nikolaidis, R.M., Prawirodirdjo, L., Miller, M., Johnson, D.J. (2004): Error analysis of continuous GPS position time series. J. Geophys. Res. 109, B03412, doi:10.1029/2003JB002741.
Ågren J. and Svensson R., 2008, Land Uplift Model and System Definition Used for the RH 2000 Adjustment of theBaltic Levelling Ring, In: Knudsen P. (Ed.), Proceedings of the 15th General Meeting of the Nordic Geodetic Commission (29 May – 2 June 2006), DTU Space, 84–92.
Mr. Pasi Häkli
Finnish Geospatial Research Institute (FGI) / National Land Survey of
Finland Geodeetinrinne
2 Kirkkonummi
FINLAND
https://www.maanmittauslaitos.fi/en/research