

Article of the Month - June 2020 |
Asmae Azzioui, Moulay Hafid Bouhamidi, Mustapha Mouadine And Mohammed Ettarid, Morocco
 |
 |
 |
 |
| Asmae Azzioui | Moulay Hafid Bouhamidi | Mustapha Mouadine | Mohammed Ettarid |
This article in .pdf-format (16 pages)
This peer review paper should have been presented at the FIG Working Week 2020, Amsterdam, Netherlands. The paper is about how the current Moroccan energy policy aims to develop and promote renewable and clean energy.This article traces all the results of research and practical manipulations carried out within this project.
The current Moroccan energy policy aims to develop and promote renewable and clean energy. To this end, one of the Morocco's most available energies that could contribute appreciably to improving national energy mix is solar energy. Thus, any solar project must rely (at least in large part) on modeled (satellite-based) irradiance data. However, a key question remains: the reliability of these data sets and generated maps. Therefore, our study comes to highlight the problems with the assessment of the solar resource and to stress the concept of the calibration of satellite data (Meteosat) to ground measurements (site-specific adaptation). In order to achieve this desired goal, we have introduced the different procedures of local calibration used in the solar energy industry and operated the calibration of the Moroccan Solar Atlas (MSA). In this context, an innovative method of generalization of the calibration to cover the entire territory of Morocco has been implemented and has demonstrated the quality of the proposed method and its contribution compared to conventional methods.
Masen (The Moroccan Agency for Sustainable Energy) is responsible for managing renewable energy in Morocco and leads development programs of integrated projects aimed at creating an additional 3,000 MW of clean electricity generation capacity by 2020 and a further 6,000 MW by 2030.The goal is to secure 52% of the country’s energy mix from renewable sources by 2030. The site exploration direction is involved early in the project development process, in order to identify the land best suited to hosting energy complexes. It is responsible for assessing the natural resources (implementation notably of the MSA) and all other meteorological conditions (pressure, wind speed, temperature, rainfall and humidity). Thus, the deployment of any solar technology begins with the implementation of a solar information system that will allow access to the dynamic values of the various components of solar radiation called the solar atlas representing the mapping of the different components of solar radiation. Solar parameters are GHI (Global Horizontal Irradiance), DNI (Direct Normal Irradiance) and DHI (Diffuse Horizontal Irradiance). The development of the solar atlas involves the development of methods of treatment and analysis of different components of solar radiation from satellite data (reflectance). However, satellite imagery tends to underestimate or overestimate the values of solar irradiance (GeoModel Solar, 2013). The result is the need to calibrate these data and adapt them to the ground values based on in-situ measurements acquired by seven kingdom-wide stations (Boujdour, Laayoune, Tata, Midelt, Ouarzazate, Taznakht and Ain Beni Mathar), since local ground data acquired by ground-based measuring instruments are much more accurate than satellite models (2% versus 5-15%). This local adaptation procedure is thus essential to obtain the best possible solar resource data.
This paper traces all the results of research and practical manipulations carried out within this project. The first part is devoted to the presentation of the state of art of the main methods used in the local calibration of satellite data. This review is based on application examples found in articles and publications and on formalizations corresponding to different domains (the wind industry). From this study, the methods that will be applied to MSA will emerge. Thus a second axis will expose all the practical manipulations as well as the presentation and the analysis of the results. From these conclusions, we will see what perspectives are envisaged and their interest and importance for the continuation and improvement of the results of this project.
The calibration consists of adjusting a "time series" of long-term spatial modeled long-term irradiation satellite data, to time series of punctual accurate and high-quality short-term in-situ measurements through the determination of a set of parameters and calibration coefficients. Local correlations and adaptations of modeled irradiances should only be applied under the following conditions (Badger et al., 2012):
The different procedures could be classified in 3 groups, according to the approach used to treat the calibration process, as follows:
1. Statistical approach of adaptation applied to previously derived GHI and DNI (Fig. 1). Two variants of this approach had been presented, namely the quotient (Gueymard et Wilcox 2009) and the regression of the cumulative frequencies (Meyer et al. (2012).

2. Physical Approach: Adaptation approach of input data of the satellite model with re-application of the model on the satellite images to eliminate the systematic errors. Wey et al. (2012).
If we want to compare the two previous approaches (Fig. 2), we can say that the first one is
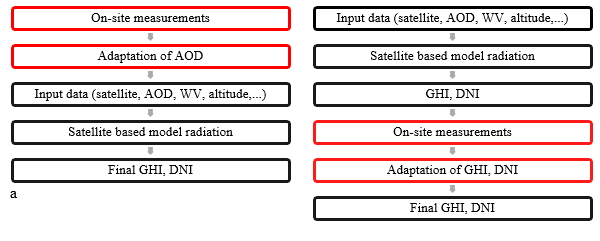
downstream correction of the irradiations while the second is an upstream adaptation of the input data of the satellite model
Figure 2. Comparison between the physical (left) and statistical approach (right)
3. Statistical approach based on advanced techniques commonly used in numerical weather prediction methods NWP, such as Measure-Correlate-Predict (MCP) Stoffel et al. (2010), and Model Output Statistics (MOS) Thuman et al. (2012), (Bender et al., 2011).
This method is based on the calculation of the quotient between the modeled and measured values for the common period. This ratio is calculated on a monthly basis and is considered constant throughout the month in question and applied systematically every hour (or even hourly subintervals) during that month (Leloux et al., 2014):
![]()
m is the month of the year from 1 to 12, DNIm, MEAS is the monthly value of the DNI measured by the in situ radiometer, DNIm, DB is the corresponding modeled value provided by the database and δm is the bias between the measured data and the modeled data. The estimated biases are then applied to correct the long-term data:
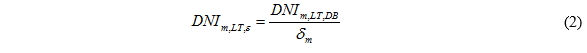
DNIm, LT, DB is the long-term value of DNI contained in the database and DNIm, LT, ε is the corresponding value corrected by the present method
TABLE 1. Strengths and weaknesses of the quotient’s method

In this method and for the whole common period, the measured frequency distributions are evaluated and considered as reference (Fig. 3), on which are then adapted those of modeled irradiances. (Sùri et al., 2010)
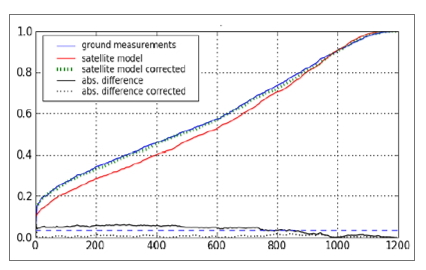
Figure 3. Comparison between the physical (left) and statistical approach (right)
TABLE 2. Strengths and weaknesses of the feature transformation approach

This is in fact an approach quite similar to the previous method because it tends to reduce the main statistics (bias, RMSD and KSI), but the adaptation is done here at the level of the input data Wey et al. (2012). For our case, since we have neither physical models nor their input data, we cannot apply the method of adaptation of input data.
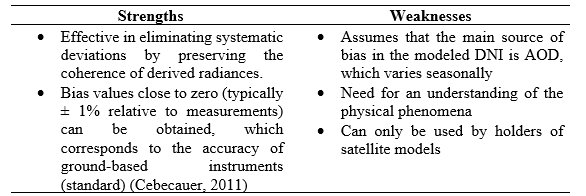
TABLE 3. Strengths and weaknesses of the physical approach
2.2.4 Weighted Average Method or Method of Combining Satellite Data and Ground Measurements
The idea is to calculate a weighted average of all input data (in situ measurements and modeled satellite data) over a certain parallel period (Meyer et al., 2008). This average is considered the best estimate of the input datasets. Since the high accuracy of the in situ data will be transferred to the time series of the satellite. It can be calculated by formula 3:
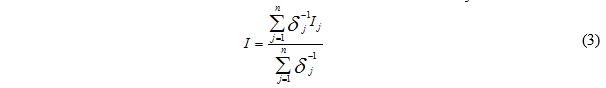
We take the inverse of the uncertainty of the measurement δ of each set of data j as a weight, where j is a set of individual data for a particular site, and n is the total number of independent datasets. This approach combines proportionally with the quality expressed by the uncertainty δj, the n data sets. Once the average is calculated, it is necessary to identify the relationship between the adjusted data and the raw satellite data to apply it to the values of the raw satellite history.
TABLE 4. Strengths and limitations of the weighted average method

This method is more suited to wind than solar. It is based on a variety of statistical methods in which in situ (short-term) measurements at a new site (plant location) are linked to long-term measurements at a nearby reference site to obtain long-term estimates of the energy potential at the new site and the interannual variability (Fig. 1). In other words, the correlation is used to predict the resources for the new site. (Thøgersen et al., 2007).

Time
Figure 4. Principle of the MCP method in the wind industry
There are three types of methods (MCP), the aim is to find an equation that passes through each of the measurement points and use it to correct or interpret all the other measurements (JV Nicholas and DR White, 2001): the ratio of variance, Mortimer, and artificial neural networks (Sheppard, 2009). Of these three methodologies, only the ratio of variance is recommended for general use and only for datasets with a correlation coefficient greater than 0.8 (Sheppard, 2009). The latter was developed by Rogers et al. (2005a), in response to the aforementioned failure of linear regression. It consists in forcing the variance of the predicted irradiance at the target site to be equal to the variance measured at the target site. The predictor equation for the Ratio of Variance is as follows (Sheppard, 2009):
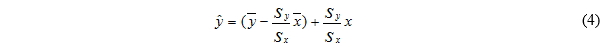
where x is the historical irradiance at the reference site, sx and sy are the standard deviations of the irradiance sample measured at the reference and target sites, respectively; and are the average of the irradiance sample at the reference and target sites, and is the predicted irradiance at the target site. As part of this study, we tried to adapt this model to the solar context while respecting its principle and its objective. One calculate for equation 4 (for each month and for each station) its parameters (the coefficient: first term of the equation and the constant: the second term of the equation) using the data of the common period in order to define the ratio of the variance model which will be applied to the monthly values of the satellite history.
![]()
Taking x is the monthly satellite irradiance of the uncalibrated history, sx and sy are respectively the standard deviations based on the daily values of the satellite irradiance and measured on site, and are respectively the monthly average calculated from the daily values of satellite irradiances and measured on site, and is the monthly satellite irradiance of the calibrated history. It should be noted that the constant term must be multiplied by the number n of days per month because it is calculated on a daily basis.
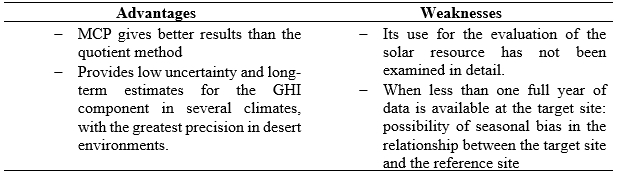
TABLE 5. Advantages and weaknesses of the MCP method
For our case study, we chose to initially apply a method simple to implement in order to easily calibrate the solar atlas and thus have preliminary conclusions. Thus, the method chosen, in view of its simplicity, is the quotient. Moreover, given the robustness of the ratio of variance method, which is one of the variants of the MCP approach, we have chosen, secondly, to apply it as well and to adapt it to the solar context. In order to add value to the work and to enrich the research in this modestly explored calibration field, we adopted two other methods (combination, regression by least squares) especially that it is an area still fertile with not enough references dealing with the theme.
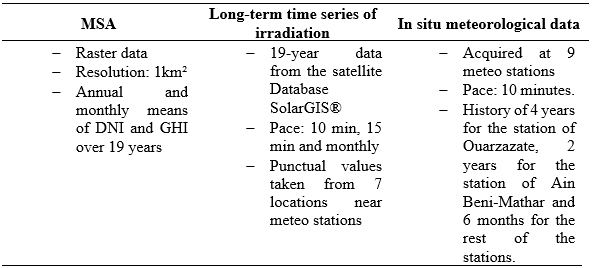
The data was provided by Masen (confidential data and property of Masen), (Table 6):
TABLE 6. Description of used datasets
The calibration process of the MSA can be summarized in 6 main steps namely (Fig.5):
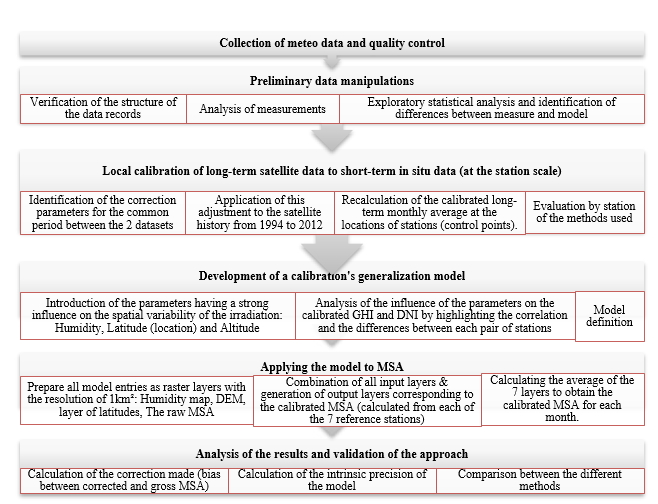
Figure 5. MSA calibration procedure
We have developed a model of the generalization of the calibration which takes into consideration certain physical parameters having a very palpable effect on the spatial variations of irradiation to ensure a certain robustness of the approach namely:
![]()
One note that the satellite database produces highly correlated GHI and DNI estimates with in-situ measurements but is usually systematically overvalued with degraded quality for stations in mountainous, humid and high aerosol concentration areas. The overall discrepancies hide a great variability of satellite estimation performance, both spatial and temporal. On the other hand, although overall concordance is good, seasonal variations exist and require a seasonal approach of calibration.

Through the results presented in these graphs (fig. 6), we clearly notice the contribution of the calibration of satellite measurements to the ground for the simultaneous period of data sets.
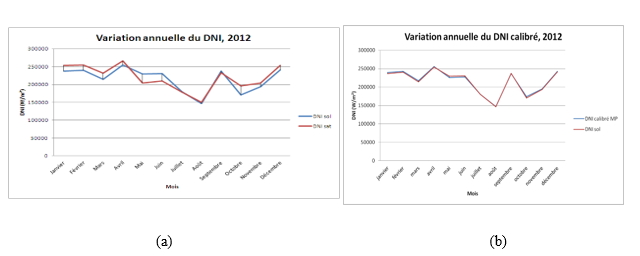
Figure 6. Comparison between monthly irradiances before (a) and after (b) calibration with in situ measurements for the 2012 common period (case of Ouarzazate station)
We notice after the analysis of the results that the ratio of the variance and quotient methods have the lowest rmsd; this corroborates their strong intrinsic precision. Moreover, the corrections made by these two approaches vary in the same direction. Moreover, following the application of the calibration coefficients of each of the regression methods and the weighted average to the historical values, we obtain some outliers and physically impossible DNI values for some stations. This proves that the model based on only one year of concomitant or less measurements does not represent the large year-to-year variations of the DNI over a period of 19 years. We have therefore decided to eliminate the methods of regression and weighted average. We also note a very significant degradation of the performance of the calibration of the DNI component compared to that, excellent of the GHI. As a result, we have chosen to generalize at the MSA scale the ratio of variance method with respect to its robustness, performance and essentially because it retains the mean and standard deviation (dispersion) for the common period. We used the quotient method to have a comparison item.
After calculating the coefficients of the model, we find that the latitude and the humidity are the parameters having a strong influence and a significant weight on the variations of irradiance, in counterpart the effect of the altitude is relatively weak because at the satellite data used have undergone altitude and shadow effects corrections. Following the calculation of the variance-covariance matrix of the model parameters for the ratio of variance and quotient method, we note that the correlation coefficients between the parameters are very negligible. Therefore, their significance cannot be to be questioned. Moreover, the accuracy of determining the coefficients of the model is high. This attests to the quality of the adjustment by least squares.
The accuracies provided by the calibration methods applied are very satisfactory and quite equivalent with higher performances for the hot and sunny months of the year (june, july, and august). It is around 0.6% for the GHI and 0.5% for the DNI. We note that for the ratio of variance method, the made corrections are negative for cold months and positive for warm months. This can be explained by the fact that the satellites underestimate irradiance for cold months as clouds reflect irradiation, and overestimate it for warmer months, hence the systematism is not constant and therefore it is compensated. Also, the negative annual correction (almost 90% of the annual irradiance corrections are centered between -13.3% and 2.5% for the DNI) reflects exactly the situation of the MSA which tends to overestimate the irradiance actually received on the surface. We also note that the corrections made to the month of January and December are the most important: these months are the only ones to deviate from the rest of the year for the Moroccan winter climate. For the quotient method, we note the existence of a positive bias (the correction is always positive) and homogeneous with the exception of December. However, this finding does not reflect exactly the reality because satellite models sometimes overestimate irradiance and sometimes underestimate it.
Based on this analysis, we recommended the adoption of the ratio of variance method for MSA calibration. Figure 7shows maps that clearly reflect the results of the ratio of variance method. One notes that the accuracy of the calibration (rmsd which is the intrinsic accuracy of the model, calculated from the 7 individual calibrated values from each station and their average) for the DNI is generally lower in coastal areas (pronounced impact of humidity on the decrease of the DNI). On the other hand, the made correction depends on the concerned geographical position: positive and decreases until it becomes negative while moving towards the south and the north. Overall the MSA has undergone a correction of 0.9% for the GHI and -6.6% for the DNI.
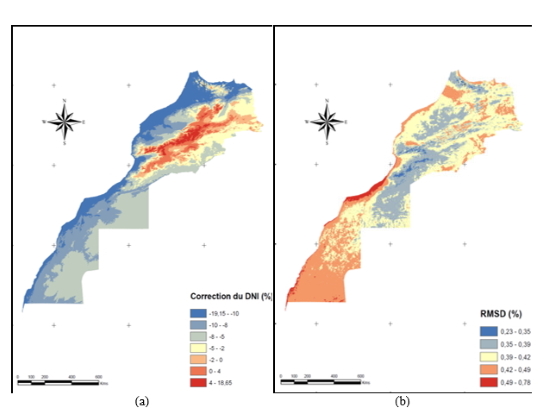
Figure 7. Correction to the annual DNI (a) Accuracy of the calibration of the solar atlas of the DNI in July (b)
In fact, in-depth resource evaluation leads to more accurate energy estimates, detailed resource analysis, and better characterization of the project site, thereby reducing project-related risks. Hence the importance of the ground-based calibration of the MSA. This work was therefore initiated by the desire to obtain solar atlases that correspond well to local conditions in Morocco and further improve their reliability. Thus this study represents only the beginning of a reflection which must be deepened and widened to improve the Moroccan Solar Atlas and its reliability. We recommend to continue this reflection and to:
This project is part of Masen's efforts to develop scientific skills by launching the "The Graduation Projects of Excellence" initiative. The idea behind this initiative was to select students on criteria of academic excellence, in partnership with universities and national schools, in order to carry out end-of-studies projects in partner companies. The objective is to constitute a first pool of skills, able to participate in the development of the solar sector in Morocco. Therefore, I would like to thank Masen for both the subject's proposal, the financial support for this work, and for the provision of solar irradiation data. The scientific supervision of the project was provided by Pr. M. ETTARID and Mr. M. H. BOUHAMIDI. May they find here the expression of my sincere gratitude for providing valuable insights and facilitating the project progress. I also express my warm thanks to Pr. Adel Bouajaj, Research Professor at The National School of Applied Sciences (Tangier), Pr. Hans-Georg Beyer from University of Agder (Norway), Pr. C. Gueymard, President of Solar Consulting Services (USA) and Mrs. J. Carow, Renewable Energy Engineer at Nordhausen University (Germany) for guiding me towards the richest bibliography.
I am Asmae Azzioui a Moroccan young surveyor engineer. I graduated from the Geomatics and Surveying Engineering School by 2014 in Rabat (Morocco) and have the pleasure to benefit from the FIG Foundation fellowship to attend and participate in the FIG congress in Malaysia held at the same year. I am working at Masen (Moroccan Agency for Sustainable energy) as a sites exploration engineer in charge of prospecting the most suitable places to locate our solar and wind power plants. For this purpose, my job is based mainly on GIS, spatial analysis, decision making, resource mapping and evaluation, etc.
Mrs Asmae Azzioui
Masen (The Moroccan Agency for Sustainable Energy)
Zenith Complex, Rabat N° 50, Rocade Sud Rabat-Casablanca A-B Buildings,
Souissi
Rabat, Morocco
Mr Moulay Hafid Bouhamidi
Masen
Mr. Mustapha Mouadine
Masen
Pr. Mohammed Ettarid
Department of Photogrammetry and Cartography, Geomatics and Surveying
Engineering School,
Hassan 2nd Institute of Agronomy and Veterinary Medicine,
Rabat, Morocco.